Dalam penelitian ini dibahas masalah antrian dengan proses kedatangan mengikuti proses Poisson dan waktu pelayanan berdistribusi eksponensial dengan dua kelas prioritas. Dengan adanya prioritas, maka pelayanan customer bersifat pre-emptive, yaitu jika terdapat customer pada kelas 1, maka server (dalam keadaan sibuk ataupun idle) akan melayani customer pada kelas 1 tersebut. Proses stokastik dimana state-nya menyatakan jumlah customer untuk setiap kelas adalah proses Markov pada state space bilangan bulat positif. Diasumsikan bahwa pemberian nomor kelas prioritas berdasarkan penurunan nomer kelasnya. Dengan kata lain, kelas 1 (sesaat setelah terdapat customer) akan mendapatkan prioritas paling tinggi untuk dilayani. Lebih lanjut, masalah antrian dengan prioritas tersebut dapat dimodelkan sebagai proses QBD (Quasi-Birth-Death) yang merupakan generalisasi dari proses Kelahiran-Kematian.
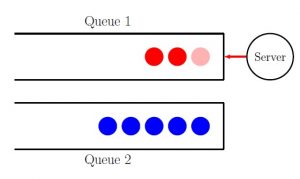
Untuk menganalisa distribusi stasioner dari proses tersebut digunakan metode Successive Lumping dan Path Counting yang memberikan solusi eksplisit. Sebagai salah satu penerapan sistem antrian dengan pemberian prioritas dalam pelayanan adalah antrian di Puskesmas (fasilitas kesehatan). Banyak puskesmas yang sudah menerapkan program Ramah Lansia, yaitu pasien yang berusia lanjut akan diberikan prioritas untuk mendapatkan fasilitas kesehatan terlebih dahulu. Dengan adanya prioritas dalam pemberian pelayanan mengakibatkan berkurangnya customer pada kelas tanpa prioritas (kelas 2) sangat bergantung pada banyaknya customer pada kelas yang diberi prioritas (kelas 1). Berkurangnya customer pada kelas 2 hanya akan terjadi jika tidak ada antrian pada kelas 1. Dengan mengetahui distribusi stasioner untuk setiap state, maka pembuat keputusan dapat menentukan rerata banyaknya customer dalam sistem. Lebih lanjut, dengan menerapkan Little’s Law dalam sistem yang stabil, dapat diketahui rerata waktu yang dihabiskan customer di dalam sistem antrian.